by Charles Dean Pruitt
(with trigonometric prompting by Katya A.)
ABSTRACT:
The
following is a method to produce formulas of various complexities
with real coeffecients
whose itereation indicate whether a given integer
is prime or composite.
METHOD:
From
theory and by inspection, composite numbers with similar
factors appear on the
number line in a periodic fashion.
Conversely prime numbers appear on the number
line irregularly as "not composites".
Therefore it is possible to find
a periodic function such as a sine curve or cycloid with
a particular periodicity
which will cross the x-axis (on a two-dimensional Cartesian
coordinate system)
at each integer whose factors correspond to that periodicity.
For purposes of
this argument the sine curve is used because it is the most familiar.
For example:
the sine curve (Sin xPi/2) has an amplitude of one and passes through
the points
on the x-axis (0,0), (2,0), (4,0), (6,0) to infinity, i.e. multiples of two.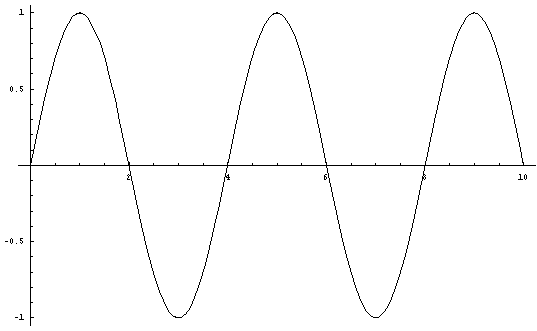
Figure
1. (Sin xPi/2)
Likewise the sine curve (Sin xPi/3) has an amplitude of
one and passes through
the points on the x-axis (0,0), (3,0), (6,0), (9,0) to
infinity, i.e. multiples of three.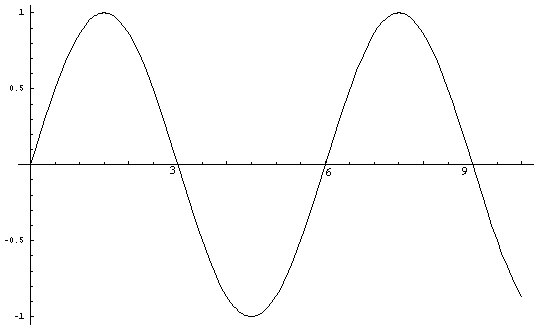
Figure
2. (Sin xPi/3)
In the same way, the sine curve (Sin xPi/5) has an amplitude
of one and passes through
the points on the x-axis (0,0), (5,0), (10,0), (15,0)
to infinity, i.e. multiples of five.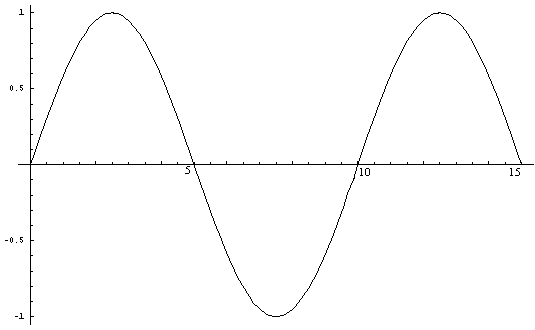
Figure
3. (Sin xPi/5)
From each of the above three figures it can be seen that
the sine curve passes through
all points on the x-axis which have its respective
prime (and periodicity) as a factor.
When Figure 1 is multiplied by Figure 2,
Figure 4 results.
This is the graph of the curve (Sin xPi/2 * Sin xPi/3).
It
is possible to see that the zero points where the curve crosses the x-axis
correspond
to the integers which have 2 or 3 or both as a factor.
Where the curve does not
intersect the x-axis at the integer values
are integers relatively prime to two
or three.
This is the case up until 'x' equals 25 or five squared.
This is
consistent with standard number theory concerning factorability.
Therefore for
the equation
Sin xPi/2 * Sin xPi/3 = 0,
the points which satisfy the equation
for 'x' are
(2,0), (3,0), (4,0), (6,0), (8,0), (9,0), (10,0), (12,0), (14,0),
(15,0),
(16,0), (18,0), (20,0), (21,0), (22,0), (24,0).
By inspection (see
Figure 4), it can be seen that there is no intersection with
the curve at the
points on the x-axis
(5,0), (7,0), (11,0), (13,0), (17,0), (19,0), (23,0).
This
is confirmed when these values for 'x' are substituted into
the equation and non-zero
answers result.
In effect these are all the primes less than five squared except
two and three.
By the above method is it possible to generate equations which
when solved for
x =0 indicate that all integers left over are primes.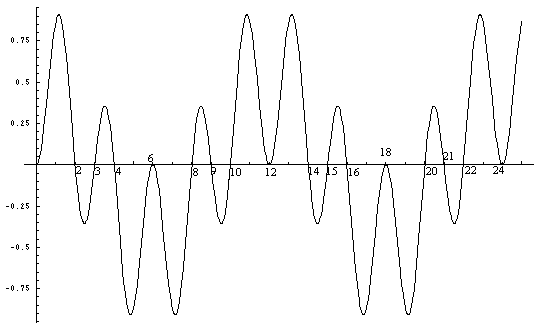
Figure
4. (Sin xPi/2 * Sin xPi/3)
In order to find the equation which will provide
the curve which
will cross the x-axis for all non-primes less than seven squared,
it
is necessary to multiply (Sin xPi/2 * Sin xPi/3 * Sin xPi/5).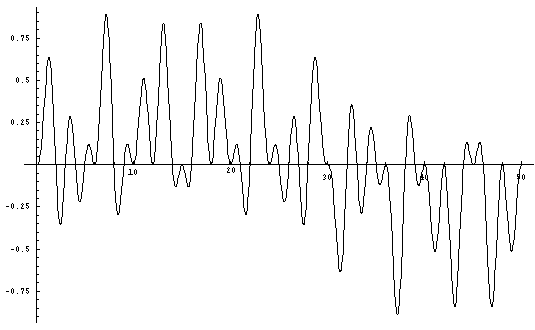
Figure
5. (Sin xPi/2 * Sin xPi/3 * Sin xPi/5)
Although it is not as clear as on
the other graphs,
it is possible to recognize the prime points on the x-axis.
Therefore
when solving for
Sin xPi/2 * Sin xPi/3 * Sin xPi/5 = 0,
the solutions for
'x' (when x<49) comprise all the composite numbers
less than 7 squared
as well as 2, 3, and 5.
Therefore all the remaining integers are prime.
With
2, 3, and 5 this constitutes all the primes less than 49.
It is possible to check
this empirically by substitution.
For exceedingly large samples it is not useful
to view a whole graph
because the fine details are not readily clear.
However
it is possible to calculate for a large range
by multiplying all the consecutive
sine curves together.
In the following example the first 27 sine curves (Sin xPi/2)
through (Sin xPi/103)
were multiplied together to yield a graph for the resultant
curve
of which 100 units are shown below.
That curve is stated as:
Sin xPi/2
* Sin xPi/3 * Sin xPi/5 * Sin xPi/7 * Sin xPi/11 * Sin xPi/13 * Sin xPi/17 *
Sin
xPi/19 * Sin xPi/23 * Sin xPi/29 * Sin xPi/31 * Sin xPi/37 * Sin xPi/41 * Sin xPi/43
*
Sin xPi/47 * Sin xPi/53 * Sin xPi/59 * Sin xPi/61 * Sin xPi/67 * Sin xPi/71
* Sin xPi/73 *
Sin xPi/79 * Sin xPi/83 * Sin xPi/89 *Sin xPi/97 *Sin xPi/101 *
Sin xPi/103
(Equation A.)
Solving the resultant equation for zero yields
all the
composite numbers up to 103 squared (10609) and
consequently all of
the primes less than 10609.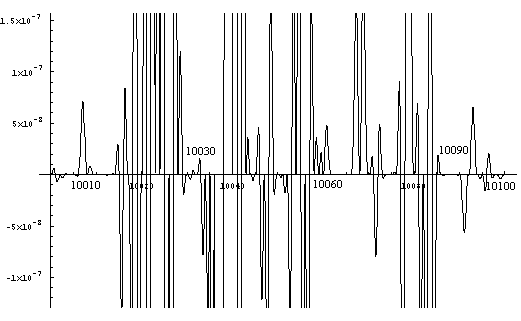
Figure
6. (Sin xPi/2* Sin xPi/3 * ... * Sin xPi/101 * Sin xPi/103)
For
purposes of illustration a small segment of the graph
is blown up (figure 7) to
shown the fine detail and confirm
visually that indeed the resulting curve crosses
the x-axis
at all the composite numbers and not at any of the primes.
However
for all values of 'x' which satisfy the equation,
results can only be derived
by solving for zero.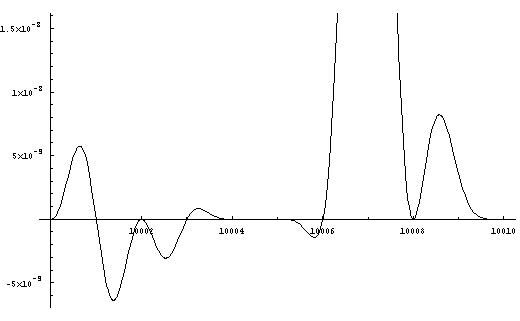
Figure
7.
It appears from this segment of the graph that 10007 and 10009
are
prime (and constitute a prime pair). This is indeed the case.
The curve between
10004 and 10006 has an amplitude of less than one ten-billionth.
With further
magnification (see Figure 8) details as fine one part in a trillion
are resolved
and indicate 10005 is composite.
(Of course there are easier methods to determine
compositeness
of numbers ending in 5.)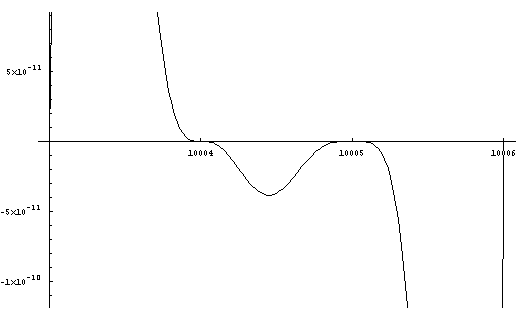
Figure
8. Detail 10003-10006
Therefore, the method to demonstrate primality or
compositeness is
to construct an appropriate equation of periodic curves multiplied
together
as above so that the final curve multiplied with all the initial curves
is
Sin xPi/A where 'A' is the first prime greater
than the square root of the number
being tested.
As a formula this reads:
Sin xPi/2*Sin xPi/3*Sin xPi/5*...*Sin
xPi/A
Substituting the number to be tested for 'x' yield zero if the number
is
a composite and a real non-zero value if the number is prime.
PROOF
Each
periodic function as defined above intersects
the x-axis at points that correspond
to all
the integers divisible by that function when y=0.
Sin xPi/2=0 represents
all integers divisible by 2.
Sin xPi3=0 represents all integers divisible by 3.
Sin
xPi/5=0 represents all integers divisible by 5.
When two functions are multiplied
together,
they will show up all the zeroes because 0 times anything is 0 .
Sin
xPi/2 * Sin xPi/3=0 represents all integers divisible by 2 and/or 3.
Sin xPi/3
* Sin xPi/5=0 represents all integers divisible by 3 and/or 5.
Sin xPi/5 * Sin
xPi/7=0 represents all integers divisible by 5 and/or 7.
There is not duplication
because 0 times 0 is 0
and hence there would be only one point indicated instead
of two.
Likewise the same argument applies when many sine curves are multiplied
together.
When all sine curves (each with periodicity corresponding to a prime
and
all such curves up to and including that whose periodicity is
less than
or equal to the square root of the largest number
in the sample space being tested)
are multiplied together,
the resultant equation gives each composite number one
time
when the equation is solved for zero.
Discarding these from the set of
integers leaves the primes.
In practice this has become a formulaic Sieve of Erastathenes.
COMMENTARY
Are
these true formulae for testing primality? Yes.
Are they useful formulae? In their
current form they are trivial.
They are computationally intensive, but the idea
of multiplying
periodic equations together and solving for zero has utility value.
Suppose
periodic equations could be constructed that were inherently simple
and when multiplied
together were likewise simple.
The restraint of computational intensity would
be diminished
with a clever enough set of periodic equations.
If non-trigonometric
periodic equations could be found,
it might produce a polynomial which could be
solved for
and produce integer roots all of which are composite.
From this
would come all the primes via solution of a polynomial
and subsequent cataloging
those integers which don't solve the equation.
By way of example, Equation A can
test
all numbers less than 10609 for primality or compositeness.
Substitute
the number to be tested for 'x'.
If the answer is zero the number is composite.
If
the answer is not zero the number is prime.
As mentioned before, the possibility
to find simpler or
more clever periodic equations would reduce the computational
intensity.
Another possibility is to choose periodic formulas where the
results
can be simplified using trigonometric identities.
Whether the computation intensiveness
can be reduced
low enough (i.e. linear instead of multiplicative or exponential)
is
an open question.
Comments: mammoth@htc.net
return
to Mathematics index
return to www.mathematical.com